Rangkuman Linked List Semester 2
Linked list :
Linked list adalah struktur data yang terdiri dari urutan catatan data sehingga setiap catatan ada bidang yang berisi referensi ke catatan berikutnya dalam suatu urutan. Linked list mengijinkan penyisipan dan penghapusan pada lokasi data dimanapun.Linked list terdiri dari 2 yaitu, Single Linked List dan Double Linked List.
Single Linked List
Single Linked List adalah sekumpulan dari node yang saling terhubung dengan node lain melalui sebuah pointer.rangkaian single linked list tersebut diawali dengan sebuah head untuk menyimpan alamat awal dan di akhiri dengan node yang mengarah pointer ke null.
Circular Single Linked List
Circular Single Linked List adalah single linked list yang pointer nextnya menunjuk pada dirinya sendiri. Jika single list tersebut terdiri dari beberapa node, maka pointer next pada node terakhir akan menunjuk ke node terdepannya.


Doubly linked list
Double Linked List adalah sekumpulan node data yang terurut linear atau sekuensial dengan dua buah pointer yaitu prev dan next. Doubel Linked List adalah linked list dengan node yang memiliki data dan dua buah referensial( biasanya disebut next dan prev ) yang menunjuk ke node sebelum dan node sesudahnya.
circular doubly linked list sama seperti circular single linked list tetapi total pointer untuk setiap node memiliki 2 point
Stack and Queue :
Stack
Stack (tumpukan) adalah struktur data yang meniru bagaimana proses menyimpan dan mengambil suatu buku pada suatu tumpukan buku yang ada di lantai. Apabila diperhatikan dengan seksama maka proses menyimpan buku (disebut push) dan proses mengambil buku (disebut pop) dari suatu tumpukan selalu dilakukan pada bagian atas tumpukan (top of the stack) sehingga terjadi urutan yang disebut LIFO (Last In First Out). Artinya, buku yang terakhir disimpan adalah buku yang pertama harus diambil karena buku inilah yang berada pada urutan teratas dari tumpukan.
Operasi dalam Stack :
Push : Menyisipkan data ke dalam stack.
Pop : Mengeluarkan data dari stack.
IsEmpty : Untuk mengecek apakah stack dalam keadaan kosong atau tidak.
IsFull : Untuk mengecek apakah stack dalam keadaan penuh atau tidak.
Clear : Mengosongkan isi data.
Queue
Queue (antrian) adalah struktur data yang meniru antrian orang yang sedang menunggu pelayanan misalnya di depan seorang teller bank, atau antrian orang yang sedang membeli karcis pertunjukan. Apabila diperhatikan dengan seksama maka penambahan orang pada suatu antrian selalu dilakukan pada urutan paling belakang (rear of queue), dan pelayanan selalu dilakukan pada urutan depan (front of queue) sehingga urutan proses antrian sering disebut FIFO(First In First Out). Yang pertama masuk antrian, itulah yang pertama dilayani.
Hash Table and Tree
Trees dan Binary tree
Tree
pemograman Tree adalah Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Struktur pohon adalah suatu cara merepresentasikan suatu struktur hirarki (one-to-many) secara grafis yang mirip sebuah pohon, walaupun pohon tersebut hanya tampak sebagai kumpulan node-node dari atas ke bawah. Suatu struktur data yang tidak linier yang menggambarkan hubungan yang hirarkis (one-to-many) dan tidak linier antara elemen-elemennya.
Ada Beberapa Jenis TREE di antaranya :
BINARY TREE
Tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal dua sub pohon dan kedua subpohon harus terpisah.
Kelebihan struktur Binary Tree :
– Mudah dalam penyusunan algoritma sorting
– Searching data relatif cepat
– Fleksibel dalam penambahan dan penghapusan data

FULL BINARY TREE
Semua node, kecuali leaf pasti memiliki 2 anak dan tiap subpohon memiliki panjang path yang sama.

COMPLETE BINARY TREE
Tree yang mirip dengan full binary tree, tapi tiap subtree boleh memiliki panjang path yang berbeda dan tiap node (kecuali leaf) memiliki 2 anak.

SKEWED BINARY TREE
Binary tree yang semua nodenya (kecuali leaf) hanya memiliki satu anak.
Contoh Pemograman Tree Sederhana di C++
#include<stdio.h>
typedef struct node{
char data;
node *kiri;
node *kanan;
};
node *akar=NULL;
addNode(node **akar, char isi) {
if((*akar)==NULL){
node *baru;
baru= new node;
baru->data = isi;
baru->kiri = NULL;
baru->kanan = NULL;
(*akar)=baru;
}
}
preOrder(node *akar) {
if(akar !=NULL) {
printf(“%c “, akar->data);
preOrder(akar->kiri);
preOrder(akar->kanan);
}
}
inOrder(node *akar) {
if(akar !=NULL) {
inOrder(akar->kiri);
printf(“%c “, akar->data);
inOrder(akar->kanan);
}
}
postOrder(node *akar) {
if(akar !=NULL) {
postOrder(akar->kiri);
postOrder(akar->kanan);
printf(“%c “, akar->data);
}
}
Hash and Hashing table:
Hash table merupakan salah satu struktur data yang digunakan dalam penyimpanan data sementara. Tujuan dari hash table adalah untuk mempercepat pencarian kembali dari banyak data yang disimpan. Hash table menggunakan suatu teknik penyimpanan sehingga waktu yang dibutuhkan untuk penambahan data (insertions), penghapusan data (deletions), dan pencarian data (searching) relatif sama dibanding struktur data atau algoritma yang lain.Hash table menggunakan memori penyimpanan utama berbentuk array dengan tambahan algoritma untuk mempercepat pemrosesan data. Pada intinya hash table merupakan penyimpanan data menggunakan key value yang didapat dari nilai data itu sendiri. Dengan key value tersebut didapat hash value. Jadi hash function merupakan suatu fungsi sederhana untuk mendapatkan hash value dari key value suatu data. Yang perlu diperhatikan untuk membuat hash function adalah:
– ukuran array/table size(m)
– key value/nilai yang didapat dari data(k)
– hash value/hash index/indeks yang dituju(h).
Source code hash table dengan linked list:
#include <stdio.h>
BINARY SEARCH TREE
Apa itu binary search tree?
Sebelum masuk ke materi kita harus paham maksud dari tree dan binary tree terlebih dahulu.Tree (pohon) adalah salah satu bentuk struktur data yang menggambarkan hubungan hierarki antar elemen-elemennya (seperti relasi one to many).Binary tree adalah tree yang hanya dapat mempunyai maksimal 2 percabangan saja.Binary Search Tree adalah struktur data yang mengadopsi konsep Binary Tree namun terdapat aturan bahwa setiap clild node sebelah kiri selalu lebih kecil nilainya dari pada root node.Begitu pula sebaliknya, setiap child node sebelah kanan selalu lebih besar nilainya daripada root node.
Aturan main binary search tree:
- Setiap child node sebelah kiri harus lebih kecil nilainya daripada root nodenya.
- Setiap child node sebelah kanan harus lebih besar nilainya daripada root nodenya.
Lalu, ada 3 jenis cara untuk melakukan penelusuran data (traversal) pada BST :
- PreOrder : Print data, telusur ke kiri, telusur ke kanan
- InOrder : Telusur ke kiri, print data, telusur ke kanan
- Post Order : Telusur ke kiri, telusur ke kanan, print data
Insert BST
Penyisipan sebuah node baru, didahului dengan operasi pencarian posisi yang sesuai. Dalam hal ini node baru tersebut akan menjadi daun/leaf.
Delete BST
Operasi delete memiliki 3 kemungkinan :
- Delete terhadap node tanpa anak/child (leaf/daun) : node dapat langsung dihapus
- Delete terhadap node dengan satu anak/child : maka node anak akan menggantikan posisinya.
- Delete terhadap node dengan dua anak/child : maka node akan digantikan oleh node paling kiri dari Sub Tree Kanan atau dapat juga digantikan oleh anak paling kanan dari Sub Tree Kiri.
AVL TREE :
AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ levelmaksimal 1 antara subtree kiri dan subtree kanan. AVL Tree muncul untukmenyeimbangkan Binary Search Tree. Dengan AVL Tree, waktu pencarian danbentuk tree dapat dipersingkat dan disederhanakan. Untuk menjaga tree tetap imbang, setelah penyisipan sebuah node, dilakukan pemeriksaan dari node baru→ root. Node pertama yang memiliki |balance factor| > 1 diseimbangkan. Prosespenyeimbangan dilakukan dengan: Single rotation dan Double rotation.
Penambahan node di AVL Tree
Untuk menjaga tree tetap imbang, setelah penyisipan sebuah node, dilakukan pemeriksaan dari node baru → root. Node pertama yang memiliki |balance factor| > 1 diseimbangkan. Proses penyeimbangan dilakukan dengan: Single rotation dan Double rotation
Single Rotation
Single rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 2. T1, T2, dan T3 adalah subtree yang urutannya harus seperti demikian serta height- nya harus sama (≥ 0). Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image) gambar 2.
Double Rotation
Double rotation dilakukan bila kondisi AVL tree waktu akan ditambahkan node baru dan posisi node baru seperti pada gambar 3. T1, T2, T3, dan T4 adalah subtree yang urutannya harus seperti demikian. Tinggi subtree T1 harus sama dengan T4 (≥ 0), tinggi subtree T2 harus sama dengan T3 (≥ 0). Node yang ditambahkan akan menjadi child dari subtree T2 atau T3. Hal ini juga berlaku untuk AVL tree yang merupakan citra cermin (mirror image) gambar 3.
Menghapus node di AVL Tree
Proses menghapus sebuah node di AVL tree hampir sama dengan BST. Penghapusan sebuah node dapat menyebabkan tree tidak imbang Setelah menghapus sebuah node, lakukan pengecekan dari node yang dihapus → root. Gunakan single atau double rotation untuk menyeimbangkan node yang tidak imbang. Pencarian node yang imbalance diteruskan sampai root.
HEAPS AND TRIES
Heaps
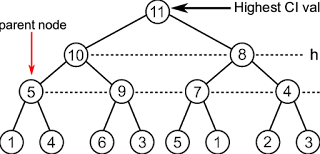
Heaps adalah struktur data yang berbasis binary tree komplit yang memenuhi properti heap.
- Min heap, dimana nilai parent harus lebih kecil dari nilai children.
- Max heap, dimana nilai parent lebih besar dari nilai children.
- Min max heap, dimana lebih mudah untuk menemukan kondisi heap min level dan max level. Setiap elemen memiliki level ganjil/genap yang lebih kecil dari semua children (MIN level), sedangkan setiap elemen yang memiliki level ganjil/genap lebih besar dari semua children (MAX level).
- Parent(x) = x / 2
- Left-child(x) = 2 * x
- Right-child(x) = 2 * x + 1
Insertion
Saat sebuah data baru dimasukkan dalam heap, maka data langsung ditempatkan di index terakhir dalam heap itu data di-uheap yang maksudnya data dibandingkan dengan parentnya. Bila lebih kecil, maka swap dengan parentnya dan dilakukan terus menerus sampai lebih besar dari parentnya. Max heap sama dengan Min heap hanya berbeda tanda lebih besar dan lebih kecil saja.
Deletion Jika dalam insertion dipakai Upheap, maka dalam deletion dipakai Downheap. Deletion dalam heap otomatis menghapus node root dari heap. Jadi, delete min dalam min heap dan delete max dalam max heap. Node yang dihapus selalu root karena merupakan note yang paling kecil sehinngga node tersebut langsung di downheap sampai ke posisinya.
Deletion Jika dalam insertion dipakai Upheap, maka dalam deletion dipakai Downheap. Deletion dalam heap otomatis menghapus node root dari heap. Jadi, delete min dalam min heap dan delete max dalam max heap. Node yang dihapus selalu root karena merupakan note yang paling kecil sehinngga node tersebut langsung di downheap sampai ke posisinya.
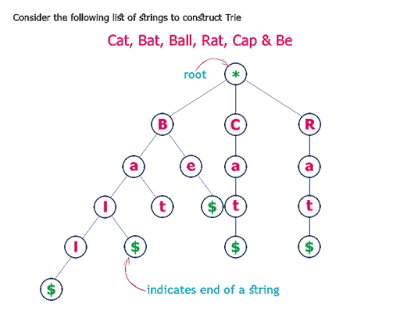
Tries
Tries adalah suatu pohon struktur data yang terurut yang menyimpan data array, biasanya string. Kata tries diambil dari kata RETRIEVAL, karena tries dapat menemukan kata tunggal dalam kamus dengan hanya awalan katanya saja.
Tries memiliki 2 property, yaitu :
- root selalu kosong
- setiap node diisi kata awalan
Sumber Referensi :
- https://kuliahinformatika.wordpress.com/2010/01/21/linked-list-definisi-node-linked-list-single-linked-list-double-linked-list-circular-linked-list/
- http://yasapurnama.blogspot.com/2015/06/stack-dan-queue-dalam-c.html
- http://www.nblognlife.com/2014/12/binary-search-tree-bst-tree-lanjutan.html
- http://dinda-dinho.blogspot.com/2013/06/penger











Comments
Post a Comment